진리 개념의 전환과 재건②
칸트철학에 단골로 등장하는 ‘선험적 종합판단’이니 ‘아 프리오리’(a priori, 선천적)니 하는 말들이 중요한 건 바로 이런 맥락에서입니다. ‘선험적’이란 말은 ‘경험적’이란 말과 반대짝입니다. ‘경험적인 것’이란 인간이 경험을 통해서 알게 되는 것입니다. 반면 ‘선험적인 것’이란 경험하지 않아도 아는 것이지요. 예를 들면 “모든 미인은 예쁘다”가 그렇습니다.
‘분석판단’은 주어에 이미 술어가 포함되어 있는 것입니다. “모든 미인은 예쁘다”라는 명제는 분석판단입니다. 왜냐하면 ‘미인’이란 주어에 이미 ‘예쁘다’라는 술어가 포함되어 있기 때문입니다. ‘종합판단’은 주어에 술어가 포함되어 있지 않은 것입니다. 예를 들어 “모든 미인은 키가 크다”는 명제가 그렇습니다. ‘미인’이란 주어를 아무리 분석해도 키가 크다는 건 알 수 없기 때문이지요..
여기서도 보듯이 분석판단은 선험적입니다. ‘미인’이란 주어에 이미 예쁘다’라는 술어가 포함되어 있으니, 경험하지 않아도 알 수 있는 거지요. 따라서 이는 언제나 타당하고 확실합니다. 그러나 대신 우리에게 아무런 지식도 추가해 주지 않지요. 미인은 예쁜 여자다’라고 정의해 놓고는 “모든 미인은 예쁘다”라고 하는 것이니, 대체 뭐 새로운 게 있겠습니까? 이런 걸 흔히 ‘동어반복’(tautology)이라고 하지요.
반면 종합판단은 대개 경험적이고 후천적입니다. 미인’들을 많이 보지 않고서는 모든 미인은 키가 크다’고 할 순 없는 일이니 말입니다. 주
어에 없는 것을 얘기하려면 대개 경험을 통해야 하지요. 따라서 주어에 없는 지식을 우리에게 추가해 주지요. 대신 언제나 타당하지도, 확실하지도 않습니다. 미인이지만 키가 작은 여자도 얼마든지 있을 수 있지 않겠습니까?


▲ 투시법적 공간
위의 그림은 1560년 경에 출판된 투시법에 관한 책에 있는 삽화다. “격자는 화가의 눈에 있는 게 아니라 세계 자체에 속해 있다”고 말하려는 것일까? 바닥과 천장, 사면의 벽이 모두 격자로 가득하다. 열린 문이나 창문의 비스듬한 평행선들은 각각 자신의 소실점에 모인다. 사람들은 이 격자로 가득한 공간 안에 있거나 그 안으로 들어온다. 정면에서 손을 번쩍 들고 들어오는 사람의 오른쪽 눈은 방 안의 평행선들이 모이는 소실점에 위치해 있으며, 그래서 격자를 만드는 선이 모이고 있지만, 이를 눈에서 격자를 만드는 선이 나오는 것으로 오해해선 곤란하다. 정면에 있는 인물의 시선에선 아무런 그물도 발사되지 않고 있을 뿐 아니라, 정면 인물의 눈에 닿는 선은 최소한으로 처리됨으로써 오히려 그는 그물 같은 저 격자의 공간 안에 사로잡혀 있음을, 그가 보는 것은 그 격자화된 공간 안에 있음을 보여준다. 아래 그림은 세를리오(Sebastiano Serlio)의 「비극을 위한 무대」(Scene for a tragedy)다. 세를리오는 좀더 세련된 스타일로 이런 격자화된 공간을 ‘객관화’한다. 그가 그린 「희극을 위한 무대」, 「비극을 위한 무대」에는 투시법에 따라 변형된 격자가 바닥의 바둑판 같은 포장도로, 건물의 벽, 기둥 등에 촘촘하게 새겨져 있다.
그런데 우리에게 새로운 지식을 추가해 주면서도 언제나 확실하고 타당한 그런 판단은 없을까? 이게 바로 칸트 고민의 핵심입니다. 선험적 명제처럼 언제나 확실하고, 종합판단처럼 새로운 걸 추가해 주는 판단은 있을 수 없는가? 이걸 칸트는 “선험적 종합판단은 가능한가?”라고 묻습니다. 그리고 그가 내린 대답은 “있다”는 것입니다. 예를 들면, “모든 삼각형의 내각의 합은 180도다”라는 판단이 그렇습니다. 알다시피 이 명제는 유클리드 기하학에선 언제나 타당하지요. 삼각형을 많이 그려 보고 각을 재 보지 않아도 이 명제는 언제나 타당합니다. 그런데 삼각형이란 주어를 분석한다고 ‘내각의 합이 180도’라는 결론은 나오지 않습니다. 즉 이 명제는 우리에게 삼각형의 성질에 대해서, ‘삼각형’이란 주어에는 없는 내용을 새로이 가르쳐주고 있는 것입니다. 따라서 종합판단이지요.
| 분석판단 | 모든 미인은 예쁘다 | 선험적 |
| 새 내용 추가 없음 | ||
| 종합판단 | 모든 미인은 키가 크다 | 후천적 |
| 새 내용 추가 | 늘 타당하진 않음 | |
| 선험적 종합판단 | 삼각형 내각의 합은 180°이다 | 선천적 |
| 새 내용 추가 | 늘 타당함 |
이같은 선험적 종합판단이야말로 인간을 진리에 도달케 해주는 판단형식이라고 합니다. 이렇듯 칸트는 진리를 밖에서 찾는 게 아니라, 언제나 올바르면서도 새로운 지식을 추가해 주는 판단형식에서, 즉 ‘선험적 종합판단’에서 찾는 겁니다. 이것이 발상의 전환을 통해 칸트가 새로이 얻은, 진리에 이르는 길입니다. 이로써 칸트는 흄에 의해 철저히 해체되었던 진리의 개념을 새로이 재건하게 됩니다.
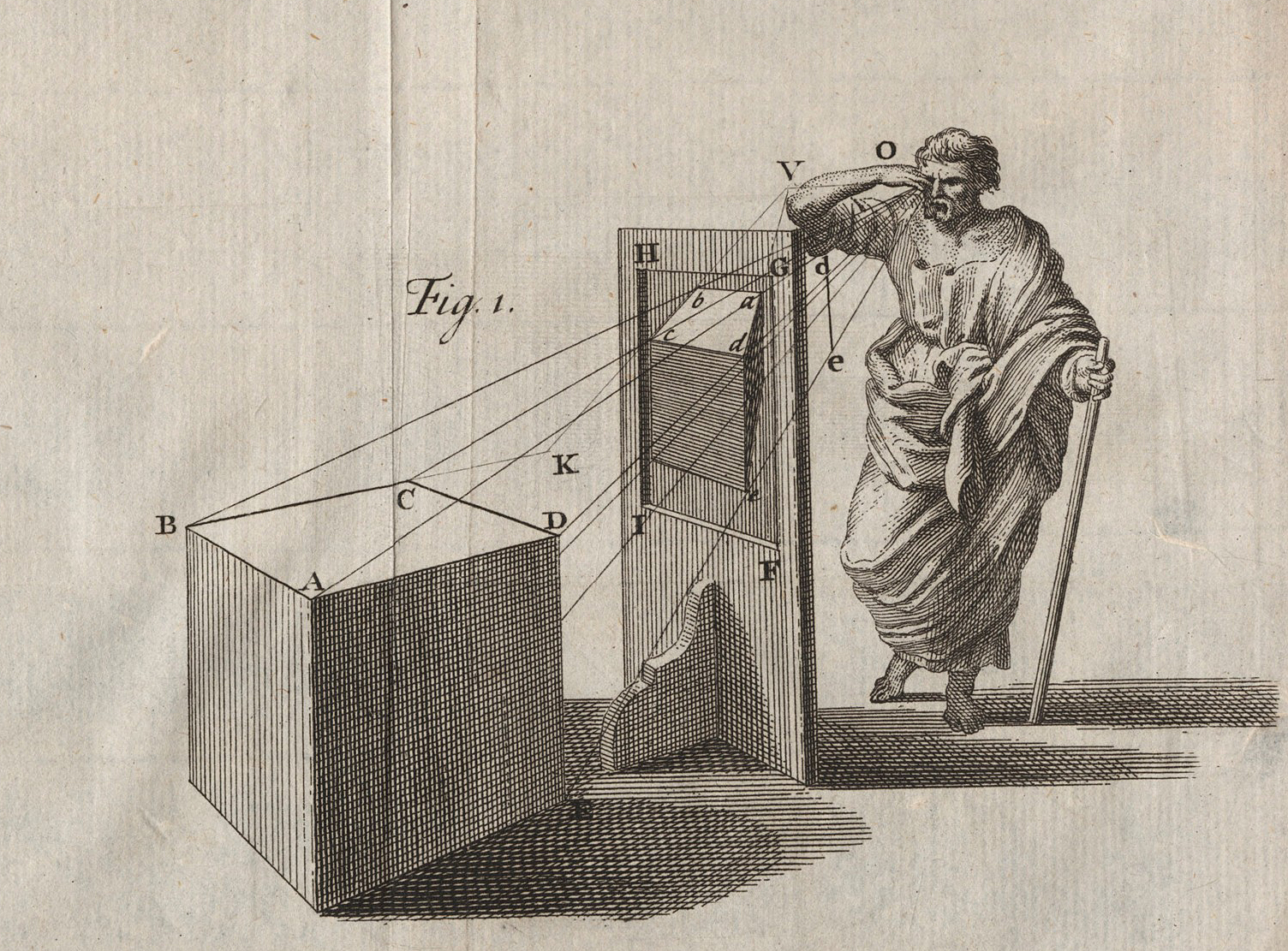
▲ 브룩 테일러, 「레오나르도의 창」
3차원의 세계를 2차원의 평면에 정확히 재현하는 방법을 ‘투시법’ (perspective)이라고 부른다. 1425년 피렌체의 브루넬레스키가 대중들 앞에서 그 정확성을 보여주는 실험을 했고, 10년 뒤 초기 르네상스의 천재 알베르티가 유클리드 기하학을 빌려 그것의 ‘과학성’을 증명한 뒤, 이 방법은 이후 거의 500년 동안 서양의 시각예술을 지배했다. 알베르티도 여기서 보이듯이 시점과 대상 사이에 화면을 놓고, 대상과 그려진 상의 비례관계가 정확히 일치함을 보여주는 식으로 ‘과학성’을 증명했다. 위 그림은 브룩 테일러(Brook Taylor)가 그린 「레오나르도의 창」(Leonardo‘s Window)이다. 그림에서 화면에 격자는 없지만, 앞서 제시된 「세계를 보는 창」과 동일한 위상을 갖고 있다. 화면에 그려진 육면체의 형상은 「세계를 보는 창」과는 달리 우리 눈이 아니라 시선이 발사되는 레오나르도의 눈에 보이는 모습이다. 그런데 테일러는 세를리오와 달리 세계를 보는 창, 그 격자란 이처럼 사물을 보는 인간의 눈 안에 있는 것임을 보여주려는 듯하다. 칸트는 이 격자와 같은 창이 누구의 눈에든 있으며, 누구의 머릿속에든 있다고 생각했다. 그것은 누구든 사물을 본다는 경험을 하려면 먼저 갖추어야 할 형식이라는 점에서 선험적’이다. 그리고 위치에 따라 형상은 달라지지만, 그 창의 격자적 형태는 변함없다는 점에서 ‘보편성’을 갖는다. 진리란 사물의 세계에 있는 게 아니라 바로 이런 선험적 주관의 형식에서 찾아야 한다는 것이 칸트의 핵심적 아이디어였다. 이를 칸트는 ‘코페르니쿠스적 전환’이라고 불렀다.
인용





